مثلث خیام :: گروه ریاضی

«مثلث خیام» را «مثلث خیام-پاسکال» و گاه به‌ندرت «مثلث خیام-پاسکال-نیوتن» نیز می‌گویند.

مثلث خیام، مثلث پاسکال، مثلث تارتالیا یا مثلث خیام - پاسکال به آرایش مثلثی شکل ضرایب بسط دو جمله ای گفته می شود.

${\binom {n}{k}}$

برای مطالعه ی خواص جمله های مثلث کافی هست از تعریف استفاده کنیم

${\binom {n}{k}}={\frac {n!}{k!(n-k)!}}$ }}}

${\binom {n+1}{k}}={\binom {n}{k-1}}+{\binom {n}{k}}$

$(a+b)^{n}={\binom {n}{0}}a^{n}+{\binom {n}{1}}a^{n-1}b+...+{\binom {n}{n}}b^{n}$

دنباله توان ۲ به صورت زیر می‌باشد

$2^{0}=1,\;2^{1}=2,\;2^{2}=4,\;2^{3}=8,\;2^{4}=16,\;...$

الگوی جالبی در داخل مثلث پاسکال برای محاسبه توان ۲ وجود دارد:

${\begin{aligned}2^{0}=1\\2^{1}=1+1=2\\2^{2}=1+2+1=4\\2^{3}=1+3+3+1=8\\2^{4}=1+4+6+4+1=16\\\end{aligned}}$

جمع عناصر هر سطر به ترتیب توان ۲ ایجاد می‌کند با توجه به رابطه (۳٫۳)اگر:

$2^{n}={\binom {n}{0}}+{\binom {n}{1}}+...+{\binom {n}{n}}(n\geq 0)$

اگر a=۱وb=-۱به رابطهٔ زیر می‌رسیم:

$0^{n}={\binom {n}{0}}-{\binom {n}{1}}+...+(-1)^{n}{\binom {n}{n}}(n\geq 0)$

در رابطه اخیر اگر n=۰قرارداد ۱=۰۰ با مشتق گیری از طرفین از طرفین رابطهٔ (۳٫۳)برای a=xوb=۱داریم $n(1+x)^{n-1}={\binom {n}{1}}+2{\binom {n}{2}}x+...+r{\binom {n}{r}}x^{r-1}+...+nx^{n-1}$

حال اگر x=۱یا x=-۱باشد

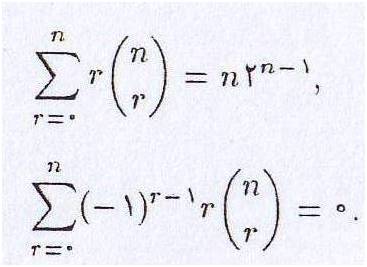
با مشتق گرفتن از مراتب بالاتر از رابطهٔ (۴٫۳)به روابط دیگری دست می‌یابیم با تعویض عمل مشتق گیری با روابط دیگری به دست می اید.

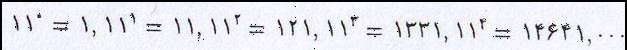
در حالت کلی اگر جمله‌های سطر nام مثلث را از راست به چپ از دیدگاه تعداد یکان دهگان ... نگاهکنیم وبدین طریق عدد Nnرابسازیم طبق اتحاد دو جمله‌ای خیام عدد Nnتوانی از ۱۱ است

مثلاً:

در مورد سطر ۷ام دقت کنید. الگوی زیر رعایت شده.

در مثلث پاسکال قطر از اعداد طبیعی، قطر ۲ از اعداد مثلثی وقطر۳ از اعداد ۴وجهی تشکیل شده‌اند.

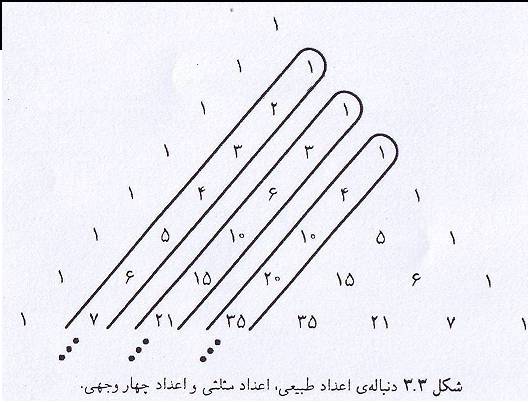
با نگاه به قطرهای مثلث ملاحظه می‌شود که هر عدد مثلثی مجموع چند عدد طبیعی وهر عدد ۴ وجهی مجموع چند عدد مثلثی است. به طور کلی می‌توان گفت که قطر kام از اعداد مصور kبعدی تشکیل شده‌اند که به صورت (c(n,kمی‌باشد. در ضمن داریم:

${\binom {n}{k}}={\binom {n-1}{k-1}}+{\binom {n-2}{k-1}}+...+{\binom {k-1}{k-1}}$

دنبالهٔ فیبوناتچی

اگر قطرها را با شیب بیشتر انتخاب کنیم.داریم:

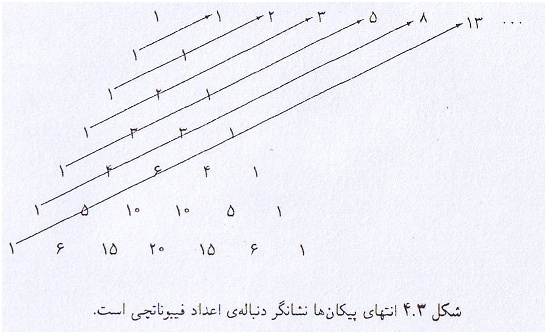
مجموعه اعداد روی قطر ها دنباله ی :

   ...و13و8و5و3و1و1

تشکیل می دهد.در این دنباله جمله اول ودوم 1 است بقیه جملات جمع دو جمله قبلی اش می شوند

F1=F2=1    Fn+2=Fn+1+Fn

اثبات این خاصیت به وسیله مثلث به راحتی قابل مشاهده است. اگرشیب قطر های فیبوناچی را بیشتر کنیم.به تعمیمی از این دنباله دست خواهیم یافت

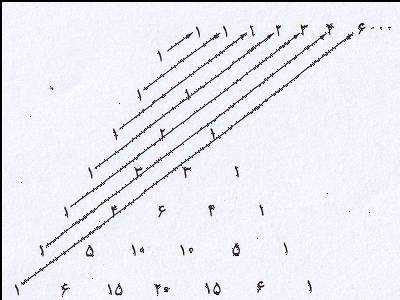
اگر ان را با Gn نمایش دهیم داریم

 G1=G2=G3=1  Gn+2=Gn+1+Gn-1

تعمیم های مختلف از دنباله فیبوناچی داریم.

دنباله واقع بر عمود منصف مثلث را به صورت زیر در نظر می‌گیریم... و۲۵۲و۷۰و۲۰و۶و۲و۱
${\begin{aligned}1=1^{2}\\2=1^{2}+1^{2}\\6=1^{2}+2^{2}+1^{2}\\20=1^{2}+3^{2}+3^{2}+1^{2}\\70=1^{2}+4^{2}+6^{2}+4^{2}+1^{2}\\...\end{aligned}}$

تعمیم دنباله بالا به صورت زیر است:

${\binom {2n}{n}}={\binom {n}{0}}^{2}+{\binom {n}{1}}^{2}+{\binom {n}{2}}^{2}+...+{\binom {n}{n}}^{2}(n\geq 0)$

به عبارت دیگر مجموع مربعات جمله‌های سطر ان ام برابر است با رآس تحتانی یک لوزی که این لوزی که این سطر یکی از قطرهای ان می‌باشد.

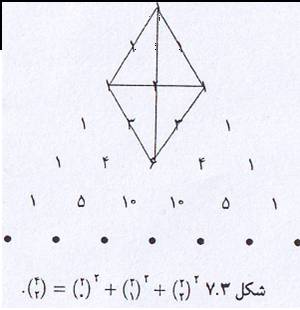
ویژگی هندسی فانگ

ایا دو عدددر مثلث پاسکال می توان یافت که مجموع یا تفاضلشان مربع کامل باشد؟ عناصر واقع در قطر 3، اعداد مثلثی هستندو نیز مجموع 2 عدد مثلثی متوالی یک مربع کامل است.اگر Tnنشان دهنده nامین عدد مثلثی باشد.داریم:

Tn+Tn+1=n2

واین نتیجه می دهد.

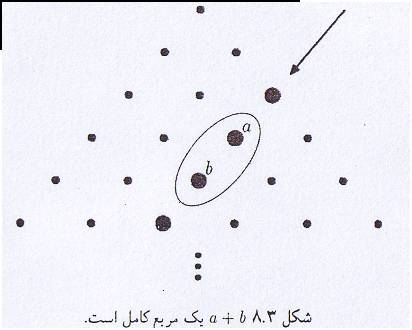
برای تفریق داریم

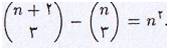
ویژگی چوب چوگان

تساوی زیر را در نظر بگیرید.
${\binom {n}{0}}+{\binom {n+1}{1}}+{\binom {n+2}{2}}+{\binom {n+3}{3}}={\binom {n+4}{4}}$

اگر هر کدام از عناصر دو طرف تساوی را به صورت نقاط هندسی در نظر بگیرید

اگر طول چوب چوگان را کا در نظر بگیریم رابطه بالا را تعمیم دهید

ضرب صلیبی

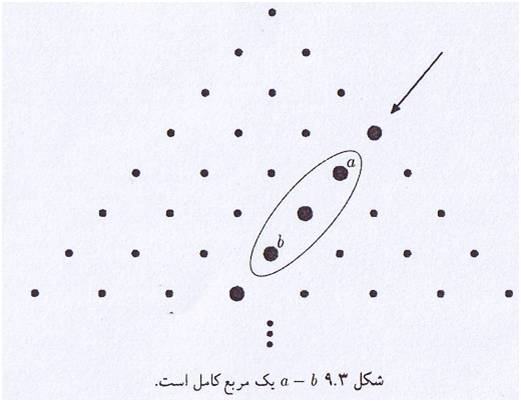
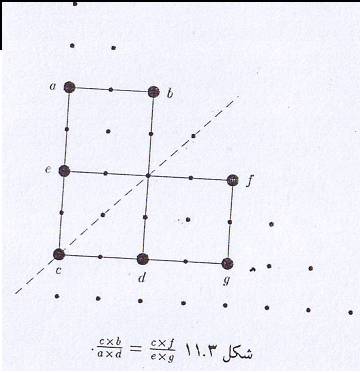
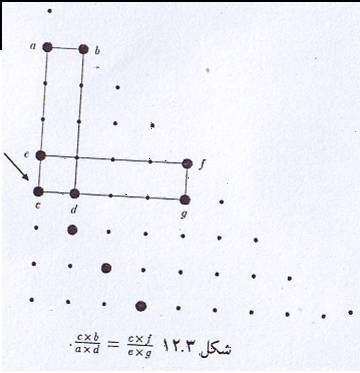
در اینجا مستطیل هایی را به صورت قائم الزاویه و افقی در داخل مثلث خیام در نظر می گیریم.رئوس این مستطیل ها که بر روی درایه های این مثلث واقع شده اند در اینجا رابطه ای بر حسب درایه های واقع بر رئوس این مستطیل به دست می اوریم. نکته جالب این است که با لغزاندن مستطیل به نحوی که نقطه ی cدر طول قطر (در امتداد پیکان)جا به جا شود

 (a*d)/(c*b)یک مقدار ثابت خواهد بوذ

ستارهٔ داود

در خاصیت ضرب صلیبی اگر به جای مستطیل ها یک ستاره به صورت زیر در نظر بگیریم به قسمتی که رئوس ان بر درایه های مثلث خیام قرار گیرند.به تساوی زیر میرسیم:
${\binom {n-2}{r+1}}{\binom {n-1}{r}}{\binom {n}{r+2}}={\binom {n-2}{r}}{\binom {n}{r+1}}{\binom {n-1}{r+2}}$

در مرکز این ستاره عنص ${\displaystyle {\binom {n-1}{r+1}}}$ ${\binom {n-1}{r+1}}$ قرار دارد

حال با این توضیح مختصر در مورد برخال‌ها برمی‌گردیم به «مثلث خیام – پاسکال». در مورد این مثلث زیاد شنیده‌ایم از جمله در مورد کاربرد فراوانش در نظریه‌ی اعداد و ترکیبیات. حال می‌خواهم یکبرخال ساده را در این مثلث به شما نشان دهم. موضوعی که باعث می‌شود این مثلث جایی را نیز در دنیای برخال‌ها یعنی سیستم‌های دینامیکی پیدا کند. مسئله خیلی ساده است، تمام اعداد زوج را در «مثلث خیام – پاسکال» پاک کنید، آن‌چه باقی می‌ماند برخالی معروف است با نام «مثلث سرپینسکی»:

گروه ریاضی

مدرسه شهیدبهشتی بروجن